by
on
under ,
tagged ,
∞ Permalink

Appendix of the Jeffreys’s paper

Posted on by

The following calculations are based on Jeffreys’s (1961, p. 269) Theory of Probability and elaborates why he choose to use a symmetric proper weighting function \pi_{1}(\delta) on the test relevant parameter the population effect size \delta={\mu \over \sigma}.

First, to relate the observed t-value to the population effect size \delta within \mathcal{M}_{1}, Jeffreys rewrote the likelihood of \Mc_{1} in terms of the effect size \delta and \sigma. To calculate the weighted likelihood of \Mc_{1} he then choose to set \pi_{1}(\delta, \sigma) = \pi_{1}(\delta) \pi_{0} (\sigma). By assigning the same weighting function to \sigma as was done for \mathcal{M}_{0}, we obtain:

(1)   \begin{align*} p(d \, | \, \mathcal{M}_{1}) = (2 \pi)^{-{n \over 2}} \int_{0}^{\infty} \sigma^{-n-1} \int_{-\infty}^{\infty} \exp \left ( - {n \over 2} \left [ \Big ({\bar{x} \over \sigma} - \delta \Big )^{2} + \Big ({s \over \sigma} \Big )^{2} \right ] \right ) \pi_{1}(\delta ) \, \text{d} \delta \, \text{d} \sigma. \end{align*}

The remaining task is to specify \pi_{1}(\delta), the weighting function for the test-relevant parameter. Jeffreys proposed his weighting function \pi_{1}(\delta) based on desiderata obtained from hypothetical, extreme data.

Predictive matching: Symmetric 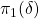\pi_{1}(\delta)

The first “extreme” case Jeffreys discusses is when n=1; this automatically yields s^{2}=0 regardless of the value of \bar{x}=x. Jeffreys noted that a single datum cannot provide support for \mathcal{M}_{1}, as any deviation of \bar{x} from zero can also be attributed to our lack of knowledge of \sigma. Hence, nothing is learned from only one observation and consequently the Bayes factor should equal 1 whenever n=1.

To ensure that \text{BF}_{10} = 1 whenever n=1, Jeffreys (1961, p. 269) entered n=1, thus, \bar{x}=x and s^{2}=0 into Eq. 2 and noted that p(d \, | \, \mathcal{M}_{1}) equals p(d \, | \, \mathcal{M}_{0})={1 \over 2 |x|}, if \pi_{1}(\delta) is taken to be symmetric around zero. The proof assumes that x > 0 and uses the transformation \xi = {x \over \sigma}, thus, \sigma={ x \over \xi } and \xi^{-1} \text{d} \xi = -\sigma^{-1} \text{d} \sigma. Hence, by symmetry of \pi_{1}(\delta) we get

(2)   \begin{align*} (2 \pi)^{1 \over 2} p(d \, | \, \mathcal{M}_{1}) = & \int_{0}^{\infty} \sigma^{-1} \int_{-\infty}^{\infty} \exp \left ( - {1 \over 2} \left [ (\xi - \delta )^{2} \right ] \right ) \pi_{1}(\delta ) \, \text{d} \delta \, \sigma^{-1} \text{d} \sigma \\ = & {1 \over x} \int_{0}^{\infty} \int_{-\infty}^{\infty} \exp \left ( - {1 \over 2} \left [ (\xi - \delta )^{2} \right ] \right ) \pi_{1}(\delta ) \, \text{d} \delta \, \text{d} \xi \\ = & {1 \over x} \Big [ \int_{\xi=0}^{\xi=\infty} \int_{\delta=0}^{\delta=\infty} \exp \left ( - {1 \over 2} \left [ (\xi - \delta )^{2} \right ] \right ) \pi_{1}(\delta ) \, \text{d} \delta \, \text{d} \xi \\ & + \int_{\xi=0}^{\xi=\infty} \int_{\delta=0}^{\delta=\infty} \exp \left ( - {1 \over 2} \left [ (\xi + \delta )^{2} \right ] \right ) \pi_{1}(\delta ) \, \text{d} \delta \, \text{d} \xi \Big ] \end{align*}

By swapping the order of integration (Fubini) then yields an integral in terms of \xi that yields the normalisation constant of a normal distribution, that is,

(3)   \begin{align*} p(d \, | \, \mathcal{M}_{1}) = & (2 \pi)^{-{1 \over 2}} {1 \over x} \Big [ \int_{\xi=-\infty}^{\xi=\infty} \exp \left ( - {1 \over 2} \left [ (\xi - \delta )^{2} \right ] \right ) \, \text{d} \xi \int_{\delta=0}^{\delta=\infty} \pi_{1}(\delta ) \, \text{d} \delta \Big ] \\ = & {1 \over x} \int_{0}^{\infty} \pi_{1}(\delta) \text{d} \delta = {1 \over 2 x}. \end{align*}

Hence, for \pi_{1}(\delta) symmetric around zero the weighted likelihood of P(d \, | \, \Mc_{1}) is then equal to that of the null model whenever n=1 and x>0.

Leave a Reply